Farthest Point Sampling in 3D Object Detection

Farthest point sampling (FPS) is a technique used to sample a point cloud efficiently and has been used in 3D object detection in algorithms such as Pointnet++ and PV-RCNN. FPS has better coverage over the entire pointset compared to other sampling techniques because it finds a subset of points that are the farthest away from each other. Sounds cool! But how is it done?

The algorithm

Open-MMLab’s OpenPCDet has many clear implementations of 3D object detection algorithms. I would recommend going through the repository to understand the algorithms yourself. OpenPCDet has their own implementation of FPS (linked here) which we’ll go through now.

The algorithm is written in CUDA. I’ll try and explain some of the concepts as they come up but I would recommend reading this for an excellent primer on CUDA basics.

template <unsigned int block_size>
__global__ void furthest_point_sampling_kernel(int b, int n, int m, 
    const float *__restrict__ dataset, float *__restrict__ temp, int *__restrict__ idxs) {

Let’s go through the parameters first:

• block_size: The number of threads used for each block
• b: Number of batches. Note each block is a batch
• n: Max number of points across the batches. i.e. If batch 1 has 100 points and batch 2 has 120 points, n would be 120
• m: Number of samples
• dataset: The dataset containing the pointset. Size (b X n X 3 (x, y, z))
• temp: Array to store the smallest distance between the points in the currently sampled pointset. This will be explained in more detail later. Size (b X n)
• idxs: Sampled points’ index. Size (b X m)

if (m <= 0) return;
__shared__ float dists[block_size];
__shared__ int dists_i[block_size];

Pretty self explanatory. Check if we actually need to sample any points m and declare two arrays to store results for each thread.

int batch_index = blockIdx.x;
dataset += batch_index * n * 3;
temp += batch_index * n;
idxs += batch_index * m;

Offset the pointers to point to the specified batch. Since all the data is passed in as 1D arrays, we need to offset the dataset, temp, and idxs pointers. For example, if we have 2 batches with 5 points each, the dataset pointer would be pointing to index 0 for batch 1 and index 15 (remember each point has an x, y, and z!) as shown here:

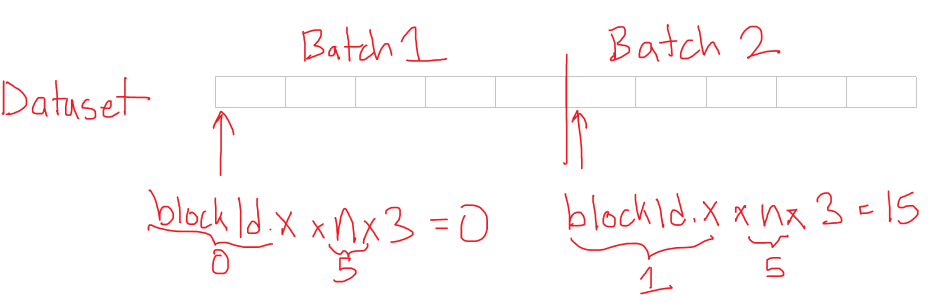
int tid = threadIdx.x;
const int stride = block_size;

int old = 0;
if (threadIdx.x == 0)
idxs[0] = old;

__syncthreads();

Now we set old to point to index 0 of the dataset. This is the first point we sample so we put it in our final sampled pointset in idxs. After, we sync threads but I think this might be unnecessary.

for (int j = 1; j < m; j++) {
    int besti = 0;
    float best = -1;
    float x1 = dataset[old * 3 + 0];
    float y1 = dataset[old * 3 + 1];
    float z1 = dataset[old * 3 + 2];

We create a for loop to sample m-1 times (Remember that the first point in each batch is chosen as the first sampled point!). We declare besti and best to keep track of the best (maximum) distance from the currently sampled pointset. To make it easier, we extract the xyz values of old into separate variables.

    for (int k = tid; k < n; k += stride) {
        float x2, y2, z2;
        x2 = dataset[k * 3 + 0];
        y2 = dataset[k * 3 + 1];
        z2 = dataset[k * 3 + 2];
        // float mag = (x2 * x2) + (y2 * y2) + (z2 * z2);
        // if (mag <= 1e-3)
        // continue;

        float d = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1) + (z2 - z1) * (z2 - z1);
        float d2 = min(d, temp[k]);
        temp[k] = d2;
        besti = d2 > best ? k : besti;
        best = d2 > best ? d2 : best;
    }

x2, y2, and z2 are just values of the candidate point k. d is the squared distance between old and k. Now we have this funky business of:

float d2 = min(d, temp[k])

To explain, we need to know what’s in temp. If we look here, we note that:

temp = torch.cuda.FloatTensor(B, N).fill_(1e10)

Okay, so temp is just array filled with 1e10 or a really large number. On the first iteration of the outer for loop (when j = 1), d2 will equal d since d < 1e10. Let’s keep a mental note of that as we’ll come back to this. We store this value in temp with:

temp[k] = d2;

besti = d2 > best ? k : besti;
best = d2 > best ? d2 : best;

Now we store the best result in besti and best. This is for when the number of points in a batch is greater than the number of threads (which is almost always the case). Let’s consider a case for 4 threads and 7 points in a batch:

The resulting best and besti would be:

Thread ID	best	besti
0	3	4
1	2	1
2	8	6
3	7	3

This for loop will be run n // block_size + 1 times for thread IDs up to n % blocksize - 1 and n // block_size times for other thread IDs.

dists[tid] = best;
dists_i[tid] = besti;
__syncthreads();

All the best (largest) distances for each thread is stored in dists and dists_i. The threads are synced to make sure dists and dists_i are fully populated.

if (block_size >= 1024) {
    if (tid < 512) {
        __update(dists, dists_i, tid, tid + 512);
    }
    __syncthreads();
}

This is pretty cool stuff. To understand this, let’s take a look at the __update function:

__device__ void __update(float *__restrict__ dists, int *__restrict__ dists_i, int idx1, int idx2){
    const float v1 = dists[idx1], v2 = dists[idx2];
    const int i1 = dists_i[idx1], i2 = dists_i[idx2];
    dists[idx1] = max(v1, v2);
    dists_i[idx1] = v2 > v1 ? i2 : i1;
}

Essentially, we split dists in half and compare the two halves against each other. The dists that are larger will be saved. The result is an array that is half the size that contains the maximum dist between tid and tid + 512. If we consider a case where block_size is 8, we would have:

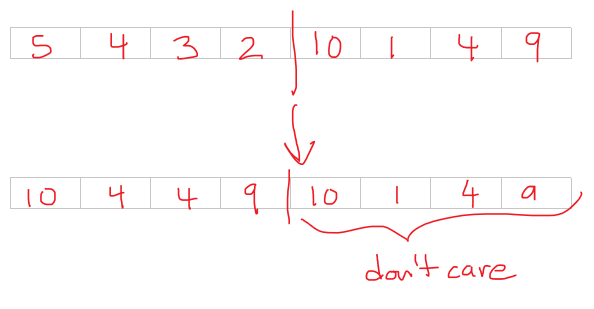
This “max halving” procedure continues until one value is left at index 0 of dists_i which is the farthest distance from old.

old = dists_i[0];
if (tid == 0)
    idxs[j] = old;
}

old is set to this farthest distance point and is stored in the sampled pointset idxs.

The second iteration

The second iteration is where things get interesting. Everything is the same until we reach:

float d2 = min(d, temp[k]);

Now, temp isn’t a default value but actually stores some other value. temp shortest distance between the currently sampled point sets. When we update temp with:

temp[k] = d2

we are calculating the shortest distance between the currently sampled point sets and the point k. What this means is that FPS maximizes the shortest distance between sampled points. masotrix says in this comment in the Pointnet++ repo:

At first it can be thought that it only uses the latest point instead of ALL the points that have already been selected, but the key is in the “temp” array (not very descriptive name) the one keeps the distance from the selected points set to every other point. As you can see, the variable “d2” is equal to the minimum between the stored distance from the selected point set and the candidate point (in “temp”), and the distance from the last point selected and the candidate point (variable “d”). In case the latter is less, the stored distance in “temp” is updated with the distance in “d2” (already equal to “d”), Note that this is made for every point, even for the ones already in the selected point set, making “temp” to have many of its elements be 0.

Everytime we encounter a point that gives us a smaller distance than what is in the current point set, we update temp with that value. This is honestly the trickiest part of the code but the use of temp makes much more sense.

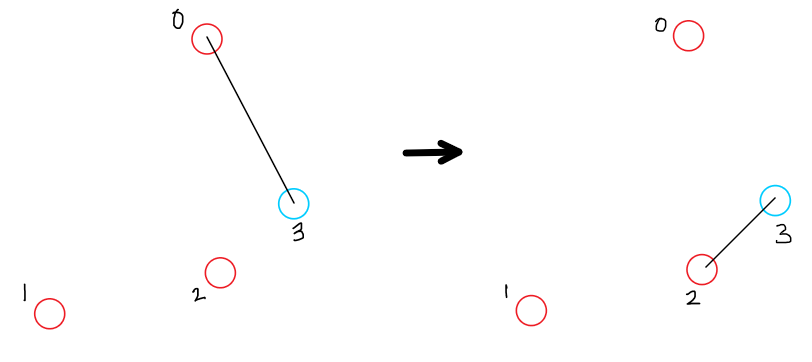
In this picture, the red circles are the current sample point set, the blue circle is the current point k and the black line represents temp[k] or the shortest distance from the previous point set to the point k. If the shortest distance between the blue and red circles is smaller than the black line, temp[k] is updated. This way, the next sampled point is always the point that is the farthest away from all the points in the current sampled point set.

Hopefully this clarifies how FPS works and how it is implemented in Pointnet++ and PV-RCNN. Thanks for reading!